
Elsősorban ez az oldal egyismeretlenes harmadfokú egyenlet megoldó kalkulátorát tartalmazza. A harmadfokú függvény ismertetése és a megoldó képlete a kalkulátor alatt található.
Első lépés, hogy a függvényt ilyen formába hozod: a·x³+b·x²+c·x+d=0
Harmadfokú függvény egy harmadrendű polinom mely 4 együtthatóból áll (a, b, c, d), az összefüggés leírható következő általános képlettel:
`f(x) = a*x^3+b*x^2+c*x+d` , ahol a, b, c és d konstansok, x pedig a változó érték.
A fenti képletnek zérushelyeit keresve, meg kell határozni azt az x értéket (vagy értékeket), melyekkre f(x)=0.
Tehát az egyismeretlenes harmadfokú egyenlet általános képlete: `a*x^3+b*x^2+c*x+d=0` ahol `a!=0`, (mivel akkor nem lenne harmadfokú az egyenlet)
Harmadfokú egyenlet ábrázolva nagyon hétköznapi nyelvvel leírva egy görbe ami három irányba is haladhat (például nő, csökken, nő). Így a görbének lehetősége van akár 3x is átmetszeni a vízszintes tengelyt, ilyenkor 3 megoldás van az x-re.
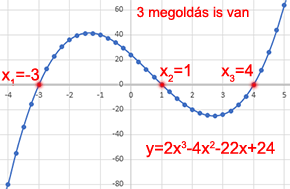
Kalkulátorban megnézhetik a fenti egyenletet, ha a=2, b=-4, c=-22, d=24 akkor x1=-3, x2=1, x3=4 eredmények jönnek ki.
De néha kétszer is irányt vált, úgy hogy nem éri el az x tengelyt, akkor csak 1 megoldás van (valós számok tartományában):
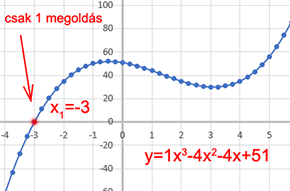
Ha a fenti képletet beírják a kalkulátorba: a=1, b=-4, c=-4, d=51, akkor x1=-3 eredmény jön ki, csak egy megoldás van.
Huhh, ezt most nagyon lerövidítem, bár így is hosszúnak nézhet ki.
`a*x^3+b*x^2+c*x+d=0` általános alakú egyenletben következő helyettesítést alkalmazunk: `x=-b/(3*a)+X`
ekkor következő formára hozható a képlet:
`X^3+(27*a^2*c-9*a*b^2)/(27*a^3)*X+(2*b^3-9*a*b*c+27*a^2*d)/(27*a^3)=0`
ahol legyen A az X szorzója, B a konstans:
`A=(27*a^2*c-9*a*b^2)/(27*a^3)`
`B=(2*b^3-9*a*b*c+27*a^2*d)/(27*a^3)`
így a következő egyenletet kapjuk:
`X^3+A*X+B=0` és ennek az egyenletnek keressük a gyökeit (milyen X-re (nagy X) lesz nulla az egyenlet értéke).
... most itt átugrok pár sort a levezetésből, és a lényegre térek... (amit átugórtam, forrásban megtekinthető [1])
A megoldóképlet diszkrimináns (Δ) értéke:
`Delta=(B/2)^2+(A/3)^3`
Ha Δ>=0, akkor egy valós megoldása lesz az egyenletnek:
`x_1=-b/(3*a)+root(3)(-B/2+sqrt(Delta))+root(3)(-B/2-sqrt(Delta))`
Ha pedig D<0, akkor 3 valós eredménye lesz:
`x_1=-b/(3*a)+2*sqrt(-A/3)*cos(1/3*arccos((-B//2)/(sqrt((-A//3)^3))))`
`x_2=-b/(3*a)+2*sqrt(-A/3)*cos((2*pi)/3+1/3*arccos((-B//2)/(sqrt((-A//3)^3))))`
`x_3=-b/(3*a)+2*sqrt(-A/3)*cos((2*pi)/3-1/3*arccos((-B//2)/(sqrt((-A//3)^3))))`
[1]: Nickalls, R. W. D. (July 2006), Viète, Descartes and the cubic equation (PDF 438 kB), Mathematical Gazette, 90: oldalak 203–208, hozzáférve 2017-01-17.
Megjegyzés: Sajnos
a kerekítési pontatlanság itt gyakori, mivel nagyon sok a "lebegőpontos" és trigonometriai művelet (cos, arccos). Minden műveletnél a kerekítési pontatlanság növekszik. Ezért is építettem be a végeredmény-ellenőrző részt a kalkulátorba. De pl. 10-10 = 0,0000000001, az majdnem 0.
Képletek megjelenítésére mathjax.org skriptet használtam.
